
Chapter 3 NHST
Following the traditional NHST approach, we consider the model previously defined that includes all effects of interest. That is the gender effect and the interaction between mother attachment and father attachment. Subsequently, we can run an analysis of deviance to evaluate the significance of the predictors using the function Anova() from the R-package car (Fox & Weisberg, 2019).
car::Anova(fit_ext_zinb)
## Analysis of Deviance Table (Type II Wald chisquare tests)
##
## Response: externalizing_sum
## Chisq Df Pr(>Chisq)
## gender 15.2947 1 9.197e-05 ***
## mother 15.6195 3 0.001357 **
## father 1.1006 3 0.776938
## mother:father 8.9096 9 0.445657
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Results indicate a statistically significant effect of gender and mother attachment. On the contrary, the interaction and father attachment are not significant. The model summary is reported below.
summary(fit_ext_zinb)
## Family: nbinom2 ( log )
## Formula: externalizing_sum ~ gender + mother * father + (1 | ID_class)
## Zero inflation: ~gender + (1 | ID_class)
## Data: data_cluster
##
## AIC BIC logLik deviance df.resid
## 3867.6 3971.9 -1911.8 3823.6 825
##
## Random effects:
##
## Conditional model:
## Groups Name Variance Std.Dev.
## ID_class (Intercept) 0.08132 0.2852
## Number of obs: 847, groups: ID_class, 50
##
## Zero-inflation model:
## Groups Name Variance Std.Dev.
## ID_class (Intercept) 0.7669 0.8757
## Number of obs: 847, groups: ID_class, 50
##
## Dispersion parameter for nbinom2 family (): 1.86
##
## Conditional model:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.01996 0.12814 7.960 1.72e-15 ***
## genderM 0.31556 0.08069 3.911 9.20e-05 ***
## motherAnxious 0.30735 0.18664 1.647 0.0996 .
## motherAvoidant 0.14496 0.25509 0.568 0.5699
## motherFearful 0.62950 0.39550 1.592 0.1115
## fatherAnxious 0.21543 0.19156 1.125 0.2607
## fatherAvoidant -0.46555 0.21138 -2.202 0.0276 *
## fatherFearful 0.07138 0.41737 0.171 0.8642
## motherAnxious:fatherAnxious -0.38346 0.26981 -1.421 0.1553
## motherAvoidant:fatherAnxious -0.09675 0.33041 -0.293 0.7697
## motherFearful:fatherAnxious -0.40811 0.49348 -0.827 0.4082
## motherAnxious:fatherAvoidant 0.34281 0.28290 1.212 0.2256
## motherAvoidant:fatherAvoidant 0.63111 0.32765 1.926 0.0541 .
## motherFearful:fatherAvoidant 0.34025 0.46490 0.732 0.4642
## motherAnxious:fatherFearful -0.04630 0.47448 -0.098 0.9223
## motherAvoidant:fatherFearful 0.11794 0.56413 0.209 0.8344
## motherFearful:fatherFearful -0.20316 0.58602 -0.347 0.7288
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Zero-inflation model:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.1239 0.2417 -4.65 3.32e-06 ***
## genderM -0.7145 0.2516 -2.84 0.00451 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1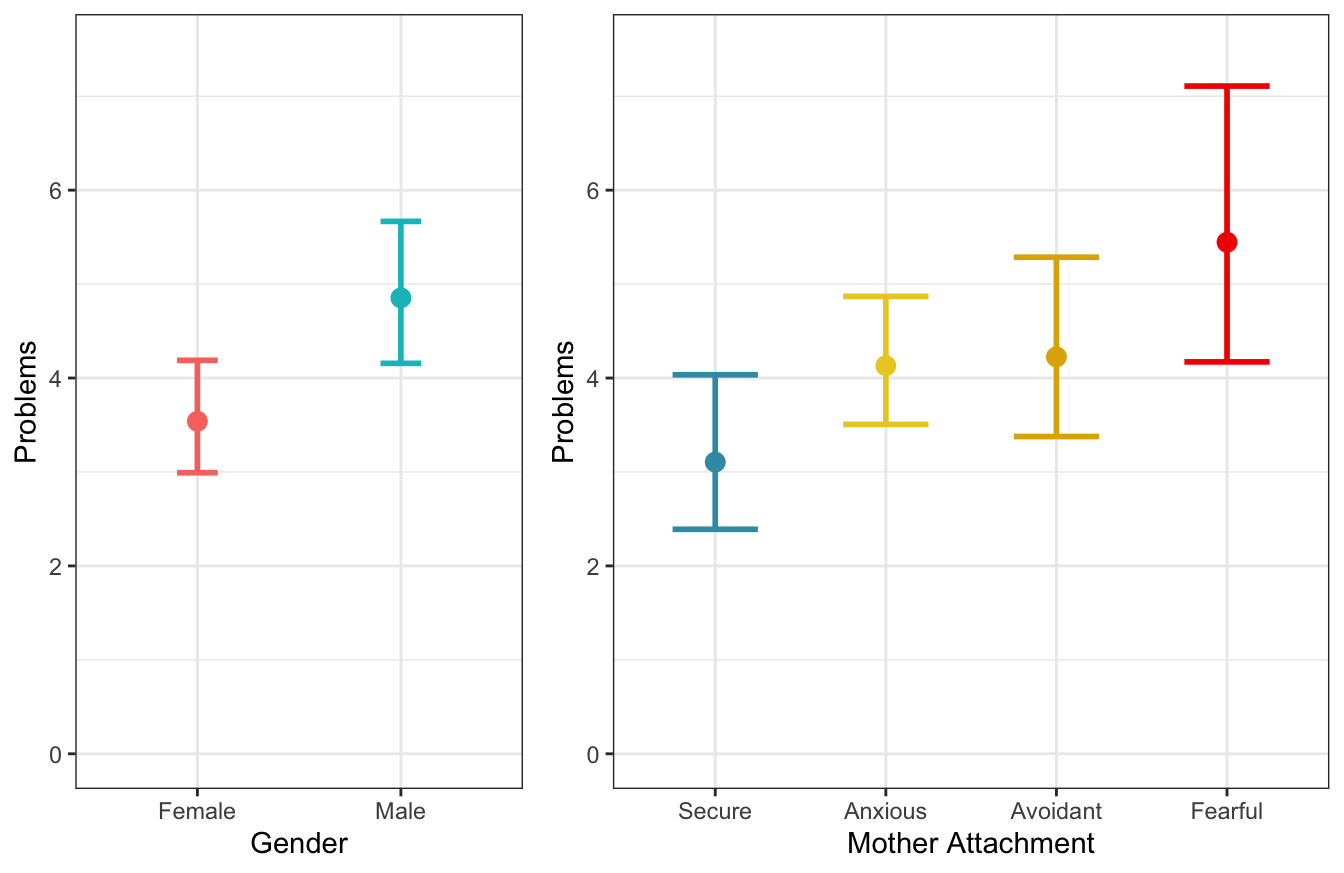
Figure 3.1: Marginal predicted values according to gender and mother attachment. Values are averaged over the other effects (\(n_{subj} = 847\)).
Post-hoc tests are run to evaluate differences between mother attachment styles. To do that we use the contrast() function from the emmeans R-package, considering pairwise comparisons and adjusting p-values according to multivariate t-distribution. This approach is less restrictive than the traditional “Bonferroni” method, as it determines the adjustment according to a multivariate t-distribution with the same covariance structure as the estimates. Results are reported below,
emmeans::contrast(emmeans::emmeans(fit_ext_zinb, specs = ~ mother ),
"pairwise", adjust = "mvt")
## NOTE: Results may be misleading due to involvement in interactions
## contrast estimate SE df t.ratio p.value
## Secure - Anxious -0.2856 0.140 825 -2.034 0.1719
## Secure - Avoidant -0.3080 0.162 825 -1.902 0.2229
## Secure - Fearful -0.5617 0.178 825 -3.149 0.0088
## Anxious - Avoidant -0.0224 0.124 825 -0.181 0.9978
## Anxious - Fearful -0.2761 0.146 825 -1.885 0.2299
## Avoidant - Fearful -0.2537 0.167 825 -1.522 0.4180
##
## Results are averaged over the levels of: gender, father
## Results are given on the log (not the response) scale.
## P value adjustment: mvt method for 6 testsOverall, results indicate that Males have more externalizing problems than Females and, regarding mother attachment, Fearful children have more problems than Secure children.
To evaluate the fit of the model to the data, we used \(R^2\). In the case of generalized mixed-effects models, however, there are several definitions of \(R^2\). We computed the Marginal \(R^2\) and the Conditional \(R^2\) as suggested by Nakagawa et al. (2017). Marginal \(R^2\) is concerned with the variance explained by fixed factors of the model, and Conditional \(R^2\) is concerned with the variance explained by both fixed and random factors of the model. To do that we use the function performance::r2().
performance::r2(fit_ext_zinb)
## Warning: mu of 4.2 is too close to zero, estimate of random effect variances may
## be unreliable.
## # R2 for Mixed Models
##
## Conditional R2: 0.191
## Marginal R2: 0.091We can see that the actual variance explained by fixed effects is almost 10%, not bad for psychology.
Conclusions
Considering attachment theoretical perspectives, results indicate only the role of mother attachment. Note, however, that traditional NHST does not allow us to evaluate evidence in favour of a hypothesis. Moreover, we actually have not tested our hypotheses but only the catch-all null hypothesis that “nothing is going on”.